Quantum circuit model
qiskit.circuit
The fundamental element of quantum computing is the quantum circuit. This is a computational routine that can be run, one shot at a time, on a quantum processing unit (QPU). A circuit will act on a predefined amount of quantum data (in Qiskit, we only directly support qubits) with unitary operations (gates), measurements and resets. In addition, a quantum circuit can contain operations on classical data, including real-time computations and control-flow constructs, which are executed by the controllers of the QPU.
You may wish to skip the introductory material and jump directly to:
- the API overview of the whole circuit module
- the detailed discussion about how circuits are represented
- the core
QuantumCircuitclass for how to build and query circuits - information on construction custom instructions
- ways to work with circuit-level objects
- discussion of Qiskit conventions for circuits, matrices and state labelling
Circuits are at a low level of abstraction when building up quantum programs. They are the construct that is used to build up to higher levels of abstraction, such as the primitives of quantum computation, which accumulate data from many shots of quantum-circuit execution, along with advanced error-mitigation techniques and measurement optimizations, into well-typed classical data and error statistics.
In Qiskit, circuits can be defined in one of two regimes:
- an abstract circuit, which is defined in terms of virtual qubits and arbitrary high-level operations, like encapsulated algorithms and user-defined gates.
- a physical circuit, which is defined in terms of the hardware qubits of one particular backend, and contains only operations that this backend natively supports. You might also see this concept referred to as an ISA circuit.
You convert from an abstract circuit to a physical circuit by using Qiskit’s transpilation package, of which the top-level access point is transpile().
In Qiskit, a quantum circuit is represented by the QuantumCircuit class. Below is an example of a quantum circuit that makes a three-qubit Greenberger–Horne–Zeilinger (GHZ) state defined as:
from qiskit import QuantumCircuit
# Create a circuit with a register of three qubits
circ = QuantumCircuit(3)
# H gate on qubit 0, putting this qubit in a superposition of |0> + |1>.
circ.h(0)
# A CX (CNOT) gate on control qubit 0 and target qubit 1 generating a Bell state.
circ.cx(0, 1)
# CX (CNOT) gate on control qubit 0 and target qubit 2 resulting in a GHZ state.
circ.cx(0, 2)
# Draw the circuit
circ.draw('mpl')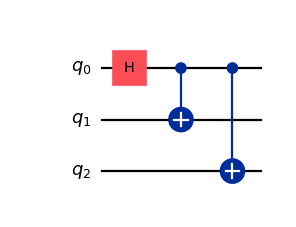
Circuit concepts and definitions
There is a lot of specialized terminology around quantum circuits. Much of this is common in quantum-computing literature, while some is more specific to quantum software packages, and a small amount specific to Qiskit. This is an alphabetical listing of some of the important concepts as a quick reference, but does not go into detail of the foundational concepts. Consider using the IBM Quantum Learning platform(opens in a new tab) if you want to start from the beginning.
abstract circuit
A circuit defined in terms of abstract mathematical operations and virtual qubits. This is typically how you think about quantum algorithms; an abstract circuit can be made up of completely arbitrary unitary operations, measurements, and potentially real-time classical computation, with no restrictions about which qubits can interact with each other.
You turn an abstract circuit into a physical circuit by using Qiskit’s transpilation package.
ancilla qubit
An extra qubit that is used to help implement operations on other qubits, but whose final state is not important for the program.
circuit
A computational routine the defines a single execution to be taken on a QPU. This can either be an abstract circuit or a physical circuit.
clbit
A Qiskit-specific abbreviation meaning a single classical bit of data.
gate
A unitary operation on one or more qubits.
hardware qubit
The representation of a single qubit on a particular QPU. A hardware qubit has some physical quantum-mechanical system backing it, such as superconducting circuits; unlike a virtual qubit, it has particular coupling constraints and only certain gates can be applied to certain groups of hardware qubits.
Qiskit does not distinguish logical qubits from any individual physical qubits when talking about hardware qubits. A QPU may implement its hardware qubits as logical qubits, where each hardware qubit comprises many physical qubits that are controlled and error-corrected opaquely to Qiskit by the control electronics. More likely, for near-term applications, a QPU will be directly exposing its physical qubits as the hardware qubits for Qiskit to reason about.
Both physical and logical qubits will have coupling constraints between them, only permit certain quantum operations on them, and have scheduling concerns between them. Qiskit abstracts these concerns together in the concept of hardware qubits. In the early days of quantum error correction, particular backends may let you access their qubit resources either as high-level logical qubits or as low-level physical qubits through Qiskit.
instruction set architecture (ISA)
The abstract model of which operations are available on which sets of hardware qubits on one particular QPU. For example, one QPU may allow and operations on all single hardware qubits, and operations on certain pairs of hardware qubits.
logical qubit
A collection of several physical qubits that are controlled together by a QPU (from the user’s perspective) to apply real-time quantum error correction. A logical qubit is a type of hardware qubit for Qiskit.
measurement
The act of extracting one classical bit of a data from a single qubit state. This is an irreversible operation, and usually destroys entanglement and phase coherence between the target qubit and the rest of the system.
physical circuit
A circuit defined in terms of hardware qubits and only the quantum operations available in a particular QPU’s ISA. Physical circuits are tied to one particular QPU architecture, and will not run on other incompatible architectures. You may also hear this referred to as an ISA circuit.
You typically get a physical circuit by using Qiskit’s transpilation routines on an abstract circuit that you constructed.
physical qubit
A controllable two-level quantum system. This is literally one “physics” qubit, such as a transmon or the electronic state of a trapped ion. A QPU may expose this directly as its hardware qubit, or combine several physical qubits into a logical qubit.
quantum processing unit (QPU)
Analogous to a CPU in classical computing or a GPU in graphics processing, a QPU is the hardware that runs quantum operations on quantum data. You can always expect a QPU that uses the circuit model of computation to be able to perform some set of gates, and measurement operations. Depending on the particular technology, they also may be able to run some real-time classical computations as well, such as classical control flow and bitwise calculations on classical data.
qubit
The basic unit of quantum information.
real-time classical computation
Any classical computation that can happen within the execution of a single shot of a circuit, where the results of the classical computation can affect later execution of the circuit. The amount of real-time classical computation available with particular QPUs will vary significantly dependent on many factors, such as the controlling electronics and the qubit technology in use. You should consult your hardware vendor’s documentation for more information on this.
unitary operation
A reversible operation on a quantum state. All quantum gates are unitary operations (by definition).
virtual qubit
An abstract, mathematical qubit used to build an abstract circuit. Virtual qubits are how one typically thinks about quantum algorithms at a high level; we assume that all quantum gates are valid on all virtual qubits, and all virtual qubits are always connected to every other virtual qubit.
When mapping to hardware, virtual qubits must be assigned to hardware qubits. This mapping need not be one-to-one. Typically, one virtual qubit will need to be swapped from one hardware qubit to another over the course of a circuit execution in order to satisfy coupling constraints of the underlying QPU. It is not strictly necessary for all virtual qubits used in a circuit to be mapped to a physical qubit at any given point in a physical circuit; it could be that a virtual qubit is measured (collapsing its state) and then never used again, so a new virtual qubit could take its place. Evaluating these conditions to map a virtual circuit to a physical circuit is the job of Qiskit’s transpilation package.
API overview of qiskit.circuit
All objects here are described in more detail, and in their greater context in the following sections. This section provides an overview of the API elements documented here.
The principal class is QuantumCircuit, which has its own documentation page, including an in-depth section on building circuits. Quantum data and the simplest classical data are represented by “bits” and “registers”:
Within a circuit, each complete CircuitInstruction is made up of an Operation (which might be an Instruction, a Gate, or some other subclass) and the qubit and clbit operands. The core base classes here are:
-
CircuitInstruction, an operation and its operands -
InstructionSet, a temporary handle to a slice of circuit data -
Operation, any abstract mathematical object or hardware instruction-
AnnotatedOperation, a subclass with applied abstract modifiers
-
The most common concrete subclass of the minimal, abstract Operation interface is the Instruction. While Operation can include abstract mathematical objects, an Instruction is something that could conceivably run directly on hardware. This is in turn subclassed by Gate and ControlledGate that further add unitarity and controlled semantics on top:
Instruction, representing a hardware-based instructionGate, representing a hardware instruction that is unitaryControlledGate, representing a gate with control structure.
Qiskit includes a large library of standard gates and circuits, which is documented in qiskit.circuit.library. Many of these are declared as Python-object singletons. The machinery for this is described in detail in qiskit.circuit.singleton, of which the main classes are each a singleton form of the standard instruction–gate hierarchy:
Some instructions are particularly special in that they affect the control flow or data flow of the circuit. The top-level ones are:
-
Barrier, to mark parts of the circuit that should be optimized independently -
Delay, to insert a real-time wait period -
Reset, to irreversibly reset a qubit to the state -
Store, to write a real-time classical expression to a storage location -
ControlFlowOp, which has specific subclasses:BreakLoopOp, to break out of the nearest containing loopContinueLoopOp, to move immediately to the next iteration of the containing loopForLoopOp, to loop over a fixed range of valuesIfElseOp, to conditionally enter one of two subcircuitsSwitchCaseOp, to conditionally enter one of many subcicuitsWhileLoopOp, to repeat a subcircuit until a condition is falsified.
Circuits can include classical expressions that are evaluated in real time, while the QPU is executing a single shot of the circuit. These are primarily documented in the module documentation of qiskit.circuit.classical. You might be particularly interested in the base classes (which are not exposed from the qiskit.circuit root):
Var, a typed classical storage location in a circuitExpr, a real-time-evaluated expressionType, the classical type of an expression.
In addition to this real-time expression evaluation, which is limited by classical hardware representations of data, Qiskit has the concept of “compile-time” parametrization, which is done in abstract symbolic algebra. These are typically used to represent gate angles in high-level algorithms that might want to perform numerical derivatives, but they are an older part of Qiskit than the real-time evaluation, so are still used in some places to do general parametrization. The main related classes are:
Parameter, the atom of compile-time expressionsParameterExpression, a symbolic calculation on parametersParameterVector, a convenience collection of manyParameters
The qiskit.circuit module also exposes some calculation classes that work with circuits to assist compilation workflows. These include:
EquivalenceLibrary, a database of decomposition relations between gates and circuitsSessionEquivalenceLibrary, a mutable instance ofEquivalenceLibrarywhich is used by default by the compiler’sBasisTranslator.
There is also a utility for generating random circuits:
Finally, the circuit module has its own exception class, to indicate when things went wrong in circuit-specific manners:
Representation of circuits in Qiskit
The main user-facing class for representing circuits is QuantumCircuit. This can be either an abstract circuit or a physical circuit. There is much more information about the QuantumCircuit class itself and the multitude of available methods on it in its class documentation.
Internally, a QuantumCircuit contains the qubits, classical bits, compile-time parameters, real-time variables, and other tracking information about the data it acts on and how it is parametrized. It then contains a sequence of CircuitInstructions, which contain the particular operation (gate, measurement, etc) and its operands (the qubits and classical bits).
Bits and registers
Qubits and classical bits are represented by a shared base Bit type, which is just intended to be a “type tag”; the classes have no behavior other than being immutable objects:
Bit
class qiskit.circuit.Bit(register=None, index=None)
Implement a generic bit.
Create a new generic bit.
Qubit
class qiskit.circuit.Qubit(register=None, index=None)
Bases: Bit
Implement a quantum bit.
Clbit
class qiskit.circuit.Clbit(register=None, index=None)
Bases: Bit
Implement a classical bit.
Qubits and clbits are instantiated by users with no arguments, such as by Qubit(). Bits compare equal if they are the same Python object, or if they were both created by a register of the same name and size, and they refer to the same index within that register. There is also a special type tag for “ancilla” qubits, but this is little used in the current state of Qiskit:
AncillaQubit
class qiskit.circuit.AncillaQubit(register=None, index=None)
Bases: Qubit
A qubit used as ancillary qubit.
A collection bits of the same type can be encapsulated in a register of the matching type. The base functionality is in a base class that is not directly instantiated:
Register
class qiskit.circuit.Register(size=None, name=None, bits=None)
Implement a generic register.
This class should not be instantiated directly. This is just a superclass for ClassicalRegister and QuantumRegister.
Create a new generic register.
Either the size or the bits argument must be provided. If size is not None, the register will be pre-populated with bits of the correct type.
Parameters
- size (int(opens in a new tab)) – Optional. The number of bits to include in the register.
- name (str(opens in a new tab)) – Optional. The name of the register. If not provided, a unique name will be auto-generated from the register type.
- bits (list(opens in a new tab)[Bit]) – Optional. A list of Bit() instances to be used to populate the register.
Raises
- CircuitError – if both the
sizeandbitsarguments are provided, or if neither are. - CircuitError – if
sizeis not valid. - CircuitError – if
nameis not a valid name according to the OpenQASM spec. - CircuitError – if
bitscontained duplicated bits. - CircuitError – if
bitscontained bits of an incorrect type.
index
name
Get the register name.
size
Get the register size.
Each of the defined bit subtypes has an associated register, which have the same constructor signatures, methods and properties as the base class:
QuantumRegister
class qiskit.circuit.QuantumRegister(size=None, name=None, bits=None)
Bases: Register
Implement a quantum register.
ClassicalRegister
class qiskit.circuit.ClassicalRegister(size=None, name=None, bits=None)
Bases: Register
Implement a classical register.
AncillaRegister
class qiskit.circuit.AncillaRegister(size=None, name=None, bits=None)
Bases: QuantumRegister
Implement an ancilla register.
A common way to instantiate several bits at once is to create a register, such as by QuantumRegister("my_qreg", 5). This has the advantage that you can give that collection of bits a name, which will appear during circuit visualizations (QuantumCircuit.draw()) and exports to interchange languages (see qasm2 and qasm3). You can also pass a name and a list of pre-constructed bits, but this creates an “aliasing register”, which are very poorly supported on hardware.
Circuits track registers, but registers themselves impart almost no behavioral differences on circuits. The only exception is that ClassicalRegisters can be implicitly cast to unsigned integers for use in conditional comparisons of control flow operations.
Classical registers and bits were the original way of representing classical data in Qiskit, and remain the most supported currently. Longer term, the data model is moving towards a more complete and strongly typed representation of a range of classical data (see Real-time classical computation), but you will still very commonly use classical bits in current Qiskit.
Instruction contexts
The scalar type of the QuantumCircuit.data sequence is the “instruction context” object, CircuitInstruction. This is essentially just a data class that contains a representation of what is to be done (its operation), and the data it acts on (the qubits and clbits).
CircuitInstruction | A single instruction in a QuantumCircuit, comprised of the operation and various operands. |
Programmatically, this class is actually implemented in Rust and is a constructed handle to internal data within Rust space. Mutations to instances of this class will not be reflected in the circuit. In general, you cannot mutate instruction contexts that are already in the circuit directly; the QuantumCircuit interface is designed for storing and building circuits, while the transpiler and its passes, and its intermediate DAGCircuit representation, are where you should look for an interface to mutate circuits.
The QuantumCircuit methods that add instructions to circuits (such as append(), and all the helper standard-gate methods) return an InstructionSet, which is a handle to several CircuitInstructions simultaneously.
InstructionSet(*[, resource_requester]) | Instruction collection, and their contexts. |
This InstructionSet is now little used in Qiskit. It provides a very minimal set of methods to perform post-append mutations on instructions (which will be propagated to the circuit), but these are now discouraged and you should use the alternatives noted in those methods.
Operations, instructions and gates
Within a CircuitInstruction, the minimal interface that any operation must fulfill is Operation. This is a very high level view, and only usable for abstract circuits. The main purpose of treating operations as Operation is to allow arbitrary mathematical objects (such as quantum_info.Operator) to be added to abstract circuits directly.
Operation() | Quantum operation interface. |
Most operations, including all operations on physical circuits, are instances of the more concretely defined Instruction. This represents any instruction that some QPU might be able to carry out natively, such as Measure. Instruction need not be unitary (much as Measure isn’t); an instruction is specifically unitary if it is a Gate.
Instruction(name, num_qubits, num_clbits, params) | Generic quantum instruction. |
Instructions can be near arbitrary, provided they only act on Qubits and Clbits, and are parametrized by their params; they should not attempt to “close over” outer circuit registers, or use hidden parameters inside themselves. Instructions can be related to other circuits to provide a decompositions by using their Instruction.definition attribute, which provides a local, one-off decomposition. This can be in whatever basis set of operations is most convenient to you, as long as the definitions of all contained gates have some topological order; that is, you cannot use a gate in a definition it its own definition depends on the parent. If the Instruction should be considered entirely opaque to optimizers, its definition can be None. See Creating custom instructions for more detail.
The params of an instruction can technically be arbitrary, but in general you should attempt to stick to parametrizations in terms of real numbers, wherever possible. Qiskit itself breaks this rule in many places, and you will find all sorts of unusual types in Instruction.params fields, but these are an annoying source of bugs because they often imply the need for type-aware special casing. If your instruction is parametrized in terms of angles, you will be able to reliably use compile-time parametrization in it, and it will integrate well with QuantumCircuit.assign_parameters().
While Instruction is not necessarily unitary, its subclass Gate implies unitarity, and adds to_matrix() and control() methods to all the methods inherited from Instruction.
Gate(name, num_qubits, params[, label, ...]) | Unitary gate. |
Gate inherits all the methods for Instruction and all the same considerations about its params and definition field, except of course that Gates cannot act on any classical resources.
Gate instances can (and should) have a base definition, but you can also specify several different decompositions in different bases by using an EquivalenceLibrary.
Subclassing Gate, Qiskit has a special ControlledGate class as well. This class is the base of many standard-library gates that are controlled (such as CXGate), which is where you are most likely to encounter it:
ControlledGate(name, num_qubits, params[, ...]) | Controlled unitary gate. |
Each of Instruction, Gate and ControlledGate has a corresponding singleton type, built using the machinery described in qiskit.circuit.singleton. The module-level documentation contains full details, along with descriptions of SingletonInstruction, SingletonGate and SingletonControlledGate. From a user’s perspective, little changes based on whether the base class is a singleton or not; the intention always remains that you should call to_mutable() first if you need to get a safe-to-mutate owned copy of an instruction (you cannot assume that an arbitrary instruction is mutable), and while direct type(opens in a new tab) inspection is discouraged, if you do need it, the reliable way to find the “base” type of a potentially singleton instruction is to use base_class.
ControlledGate uses the same mechanisms as subclassing gates to define a fixed, lazy synthesis for itself. This is naturally not hardware-aware, and harder to hook into the synthesis routines of the compiler, but works better as a concrete Instruction that could potentially be run natively on hardware. For cases where synthesis and abstract optimization is more important, Qiskit offers a composable class called AnnotatedOperation, which tracks “gate modifiers” (of which ControlModifier is one) to apply to the inner base_op.
AnnotatedOperation(base_op, modifiers) | Annotated operation. |
The available modifiers for AnnotatedOperation are:
InverseModifier
class qiskit.circuit.InverseModifier
Inverse modifier: specifies that the operation is inverted.
ControlModifier
class qiskit.circuit.ControlModifier(num_ctrl_qubits=0, ctrl_state=None)
Control modifier: specifies that the operation is controlled by num_ctrl_qubits and has control state ctrl_state.
PowerModifier
class qiskit.circuit.PowerModifier(power)
Power modifier: specifies that the operation is raised to the power power.
For information on how to create custom gates and instructions, including how to build one-off objects, and re-usable parametric gates via subclassing, see Creating custom instructions below. The Qiskit circuit library in qiskit.circuit.library contains many predefined gates and circuits for you to use.
Built-in special instructions
Qiskit contains a few Instruction classes that are in some ways “special”. These typically have special handling in circuit code, in the transpiler, or the models of hardware. These are all generally instructions you might already be familiar with.
Measurements in Qiskit are of a single Qubit into a single Clbit. These are the two that the instruction is applied to. Measurements are in the computational basis.
Measure
class qiskit.circuit.Measure(label=None)
Bases: SingletonInstruction
Quantum measurement in the computational basis.
Parameters
label – optional string label for this instruction.
Related to measurements, there is a Reset operation, which produces no classical data but instructs hardware to return the qubit to the state. This is assumed to happen incoherently and to collapse any entanglement.
Reset
class qiskit.circuit.Reset(label=None)
Bases: SingletonInstruction
Incoherently reset a qubit to the state.
Parameters
label – optional string label of this instruction.
Hardware can be instructed to apply a real-time idle period on a given qubit. A scheduled circuit (see qiskit.transpiler) will include all the idle times on qubits explicitly in terms of this Delay.
Delay
class qiskit.circuit.Delay(duration, unit='dt')
Bases: Instruction
Do nothing and just delay/wait/idle for a specified duration.
Parameters
- duration – the length of time of the duration. Given in units of
unit. - unit – the unit of the duration. Must be
"dt"or an SI-prefixed seconds unit.
The Barrier instruction can span an arbitrary number of qubits and clbits, and is a no-op in hardware. During transpilation and optimization, however, it blocks any optimizations from “crossing” the barrier; that is, in:
from qiskit.circuit import QuantumCircuit
qc = QuantumCircuit(1)
qc.x(0)
qc.barrier()
qc.x(0)it is forbidden for the optimizer to cancel out the two instructions.
Barrier
class qiskit.circuit.Barrier(num_qubits, label=None)
Bases: Instruction
A directive for circuit compilation to separate pieces of a circuit so that any optimizations or re-writes are constrained to only act between barriers.
This will also appear in visualizations as a visual marker.
Parameters
- num_qubits (int(opens in a new tab)) – the number of qubits for the barrier.
- label (str(opens in a new tab) | None) – the optional label of this barrier.
The Store instruction is particularly special, in that it allows writing the result of a real-time classical computation expression (an expr.Expr) in a local classical variable (a expr.Var). It takes neither Qubit nor Clbit operands, but has an explicit lvalue and rvalue.
Store
class qiskit.circuit.Store(lvalue, rvalue)
Bases: Instruction
A manual storage of some classical value to a classical memory location.
This is a low-level primitive of the classical-expression handling (similar to how Measure is a primitive for quantum measurement), and is not safe for subclassing.
Parameters
- lvalue (expr.Expr) – the memory location being stored into.
- rvalue (expr.Expr) – the expression result being stored.
lvalue
Get the l-value Expr node that is being stored to.
rvalue
Get the r-value Expr node that is being written into the l-value.
Real-time classical computation
Module-level documentation for how the variable-, expression- and type-systems work, the objects used to represent them, and the classical operations available.
Working with real-time typed classical data
The QuantumCircuit methods for working with these variables in the context of a single circuit.
Qiskit has rudimentary low-level support for representing real-time classical computations, which happen during the QPU execution and affect the results. We are still relatively early into hardware support for these concepts as well, so beware that you will need to work closely with your hardware provider’s documentation to get the best use out of any real-time classical computation.
These real-time calculations are represented by the expression and type system in qiskit.circuit.classical. At a high level, all real-time expressions are represented by an Expr node, which is part of an expression “tree” representation, which has a well-defined Type associated with it at every level. See the module-level documentation for much more detail on the internal representations of these classes.
The result of a real-time Expr can be used directly in certain places. Currently this is limited to conditions of IfElseOp and WhileLoopOp, and the target of SwitchCaseOp. The result can also be stored in a typed classical storage location, using the Store instruction (or its QuantumCircuit.store() constructor), backed by a expr.Var node.
A circuit can contain manual classical storage locations, represented internally by the Var node of the Expr tree. These have an attached classical type (like any other expression). These can either be declared and initialized within each execution of the circuit (add_var()), or be inputs to the circuit (add_input()).
Compile-time parametrization
Various parametric Instruction instances in Qiskit can be parametrized in ways that are designed to be resolved at compile time. These are characterized by the use of the Parameter and ParameterExpression classes.
Parameter(name, *[, uuid]) | A compile-time symbolic parameter. |
ParameterExpression(symbol_map, expr) | ParameterExpression class to enable creating expressions of Parameters. |
The main way that this differs from the expr.Var variables used in real-time classical computation is that ParameterExpression is a symbolic representation of a mathematical expression. The semantics of the expression are those of regular mathematics over the continuous real numbers (and, in limited cases, over the complex numbers). In contrast, Var is a handle to a variable stored on a classical computer, such as a floating-point value or an fixed-width integer, which are always discrete.
In other words, you can expect ParameterExpression to do symbolic simplifications that are valid in mathematics, such as simplifying . Such a simplification is not valid in floating-point arithmetic, and expr.Expr will not do this.
The “compile-time” part of these parameters means that you typically will want to “assign” values to the parameters before sending the circuit for execution. These parameters can typically be used anywhere that expects a mathematical angle (like a rotation gate’s parameters), with the caveat that hardware will usually require them to be assigned to a proper classically typed value before execution. You can do this assignment using QuantumCircuit.assign_parameters().
You may want to use many parameters that are related to each other. To make this easier (and to avoid you needing to come up with many names), you can use the convenience constructor ParameterVector. The elements of the vector are all valid Parameter instances.
ParameterVector(name[, length]) | ParameterVector class to quickly generate lists of parameters. |
Control flow in circuits
Within QuantumCircuit, classical control flow is represented by specific Instructions, which are subclasses of ControlFlowOp.
ControlFlowOp(*args, **kwargs) | Abstract class to encapsulate all control flow operations. |
These control-flow operations (IfElseOp, WhileLoopOp, SwitchCaseOp and ForLoopOp) all have specific state that defines the branching conditions and strategies, but contain all the different subcircuit blocks that might be entered in their blocks property.
IfElseOp(condition, true_body[, false_body, ...]) | A circuit operation which executes a program (true_body) if a provided condition (condition) evaluates to true, and optionally evaluates another program (false_body) otherwise. |
WhileLoopOp(condition, body[, label]) | A circuit operation which repeatedly executes a subcircuit (body) until a condition (condition) evaluates as False. |
SwitchCaseOp(target, cases, *[, label]) | A circuit operation that executes one particular circuit block based on matching a given target against an ordered list of values. |
ForLoopOp(indexset, loop_parameter, body[, ...]) | A circuit operation which repeatedly executes a subcircuit (body) parameterized by a parameter loop_parameter through the set of integer values provided in indexset. |
The SwitchCaseOp also understands a special value:
qiskit.circuit.CASE_DEFAULT = <default case>
A special object that represents the “default” case of a switch statement. If you use this as a case target, it must be the last case, and will match anything that wasn’t already matched. When using the builder interface of QuantumCircuit.switch(), this can also be accessed as the DEFAULT attribute of the bound case-builder object.
In addition to the block-structure control-flow operations, there are also two special instructions that affect the flow of control when within loops. These correspond to typical uses of the break and continue statements in classical programming languages.
BreakLoopOp(num_qubits, num_clbits[, label]) | A circuit operation which, when encountered, jumps to the end of the nearest enclosing loop. |
ContinueLoopOp(num_qubits, num_clbits[, label]) | A circuit operation which, when encountered, moves to the next iteration of the nearest enclosing loop. |
The classes representations are documented here, but please note that manually constructing these classes is a low-level operation that we do not expect users to need to do frequently.
Users should read Adding control flow to circuits for the recommended workflows for building control-flow-enabled circuits.
Since ControlFlowOp subclasses are also Instruction subclasses, this means that the way they are stored in CircuitInstruction instances has them “applied” to a sequence of qubits and clbits in its qubits and clbits attributes. This can lead to subtle data-coherence problems: the Qubit and Clbit objects used inside the subcircuit blocks of the control-flow ops will not necessarily be identical to the corresponding objects in the CircuitInstruction. Any code that consumes control-flow operations in Qiskit needs to be aware of this; within a subcircuit, you should treat subcircuit.qubits[i] as if it were really outer_instruction.qubits[i], and so on. You can generate an easy lookup table for this by doing:
cf_instruction: CircuitInstruction = ...
cf_operation: ControlFlowOp = cf_instruction.operation
for block in blocks:
# Mappings of "inner" qubits/clbits to the outer ones.
qubit_map = dict(zip(block.qubits, cf_instruction.qubits))
clbit_map = dict(zip(block.clbits, cf_instruction.clbits))
# ... do something with `block` ...Remember that you will need to propagate this information if you recurse into subblocks of control-flow operations.
All the subcircuit blocks in a ControlFlowOp are required to contain the same numbers of Qubits and Clbits, referring to the same outer bits in the same order, such that the zip loop given in the code block above works. The inner-circuit Bit objects do not need to be literally the same objects. When using the control-flow builder interface (which, it cannot be stressed enough, is highly recommended for users), the builders will arrange that the inner bit objects are identical to the outer bit objects; the qubit_map in the code block above will always be a mapping {x: x}, but if you are consuming the blocks, you should be prepared for the case that the mapping is required.
Any ClassicalRegisters used in a control-flow subcircuit must also be present in all containing blocks (i.e. any containing control-flow operations, and the outermost circuit), and all blocks in the same ControlFlowOp need to contain the same registers. Again, the builder interface will arrange for this to be the case (or produce an eager error if they cannot).
When the low-level construction is being used the inner QuantumCircuit blocks must manually close over any outer-scope real-time classical computation variables that they use. This is marked by these being in the iter_captured_vars() iterator for that block. Libraries constructing these blocks manually will need to track these captures when building control-flow circuit blocks and add them to the block using add_capture() (or the captures constructor argument), but user code will typically use the control-flow builder interface, which handles this automatically.
Consult the control-flow construction documentation for more information on how to build circuits with control flow.
Creating custom instructions
If you wish to create simple one-off instructions or gates that will be added to a circuit, and the blocks are just being used for visualization or grouping purposes, the easiest way to create a custom instruction or gate is simply to build its definition as a QuantumCircuit, and then use its to_instruction() or to_gate() method as appropriate. The results can be given directly to QuantumCircuit.append() on the larger circuit. These methods will create base Instruction or Gate instances whose definition attribute is the circuit as supplied, meaning it will automatically be accessible to the transpiler, and to other Qiskit functions that attempt to decompose circuits.
Note that standalone instructions and gates should act only on qubits and clbits; instructions that need to use complex control-flow will need to be inlined onto the QuantumCircuit using compose().
Creating instruction subclasses
The base classes Instruction, Gate and ControlledGate are all designed to be safe to subclass, and have hook points for subclasses to implement. If your custom gate is parameterless and stateless, you may also want to derive from the corresponding singleton class in qiskit.circuit.singleton, such as SingletonGate. You should consult the documentation in qiskit.circuit.singleton for additional methods and hook points for the singleton machinery.
Subclasses should typically define a default constructor that calls the :class`super` constructor with the correct arguments for your instruction. It is permissible to have extra state in the class, but your subclasses will most reliably integrate with the rest of the Qiskit machinery if you depend only on your Instruction.params, and these parameters are purely gate angles.
Subclasses of Instruction (or one of its subclasses) should implement the private Instruction._define() method, which lazily populates the hidden _definition cache that backs the public definition method.
_define
Instruction._define()
Populate the cached _definition field of this Instruction.
Subclasses should implement this method to provide lazy construction of their public definition attribute. A subclass can use its params at the time of the call. The method should populate _definition with a QuantumCircuit and not return a value.
In subclasses of ControlledGate, the _define() method should implement the decomposition only for the all-ones control state. The ControlledGate.definition machinery will modify this to handle the actual control state.
If the subclass is using the singleton machinery, beware that _define() will be called eagerly immediately after the class-body statement has been executed, in order to produce the definition object for the canonical singleton object. This means that your definition must only use gates that are already defined; if you are writing a library with many singleton gates, you will have to order your files and imports to ensure that this is possible.
Subclasses of Gate will also likely wish to override the Numpy array-protocol instance method(opens in a new tab), __array__. This is used by Gate.to_matrix(), and has the signature:
__array__
object.__array__(dtype=None, copy=None)
Return a Numpy array representing the gate. This can use the gate’s params field, and may assume that these are numeric values (assuming the subclass expects that) and not compile-time parameters.
For greatest efficiency, the returned array should default to a dtype of complex(opens in a new tab).
If your custom subclass has natural representations of its controlled or inverse forms, you may also wish to override the inverse() and control() methods.
As an example of defining a custom gate; that is, a single-angle rotation about the axis. This is essentially RZXGate, if the qubits were the other way around, so we will write our definition in terms of that. We are parametric, so cannot be a singleton, but we are unitary, so should be a Gate:
import math
import numpy as np
from qiskit.circuit import Gate, QuantumCircuit
class RXZGate(Gate):
def __init__(self, theta):
# Initialize with our name, number of qubits and parameters.
super().__init__("rxz", 2, [theta])
def _define(self):
# Our base definition is an RZXGate, applied "backwards".
defn = QuantumCircuit(2)
defn.rzx(1, 0)
self._definition = defn
def inverse(self, annotated = False):
# We have an efficient representation of our inverse,
# so we'll override this method.
return RXZGate(-self.params[0])
def power(self, exponent: float):
# Also we have an efficient representation of power.
return RXZGate(exponent * self.params[0])
def __array__(self, dtype=None, copy=None):
if copy is False:
raise ValueError("unable to avoid copy while creating an array as requested")
cos = math.cos(0.5 * self.params[0])
isin = 1j * math.sin(0.5 * self.params[0])
return np.array([
[cos, -isin, 0, 0],
[-isin, cos, 0, 0],
[0, 0, cos, isin],
[0, 0, isin, cos],
], dtype=dtype)In this example, we defined a base definition in terms of RZXGate, but to enable faster decompositions to a range of bases, we might want to add some more equivalences to SessionEquivalenceLibrary. Note that the BasisTranslator translation search will search through all possible equivalences at all possible depths, so providing an equivalence in terms of (say) XGate will automatically make decompositions in terms of RXGate available as well.
Let us add an equivalence in terms of , and for an arbitrary symbolic parameter:
from qiskit.circuit import SessionEquivalenceLibrary, Parameter
theta = Parameter("theta")
equiv = QuantumCircuit(2)
equiv.h(0)
equiv.cx(1, 0)
equiv.rz(theta, 0)
equiv.cx(1, 0)
equiv.h(0)
SessionEquivalenceLibrary.add_equivalence(RZXGate(theta), equiv)After this, for the duration of the Python interpreter session, translators like BasisTranslator will find our new definition in their search.
Working with circuit-level objects
Converting abstract circuits to physical circuits
An abstract QuantumCircuit cannot reliably be run on hardware. You might be able to use some of the high-level simulators linked to in Simulating circuits to produce quick results for small scale circuits, but to run utility-scale circuits, you will need to use real hardware, which involves compiling to a physical circuit.
The high-level function to do this is transpile(); it takes in an abstract circuit and a hardware backend or target, and returns a physical circuit. To get more access and control over the stages of the passes that will be run, use generate_preset_pass_manager() to build a StagedPassManager first, which you can then modify.
The full transpilation and compilation machinery is described in detail in the qiskit.transpiler module documentation, and detail on all the passes built into Qiskit is available in qiskit.transpiler.passes.
Simulating circuits
While not part of the qiskit.circuit interface, one of the most common needs is to get quick simulation results for QuantumCircuit objects. This section provides a quick jumping-off point to other places in the documentation to find the relevant information.
For unitary circuits, you can simulate the effects on the state by passing the QuantumCircuit directly to the Statevector default constructor. You can similar get a unitary matrix representing the circuit as an operator by passing it to the Operator default constructor. If you have a physical circuit, you may want to instead pass it to Operator.from_circuit() method to apply transformations from the QuantumCircuit.layout to map it back to the “abstract” qubit space.
For a more backend-like simulation experience, there are simulator-backed implementations of all the Qiskit hardware interfaces. In particular, you might be interested in:
BasicProviderand the raw backends it can return to you.StatevectorSimulatorfor a backend-like wrapper aroundStatevector- The
qiskit_aer(opens in a new tab) for full, high-performance simulation capabilities. StatevectorSamplerandStatevectorEstimatorfor simulator-backed reference implementations of the Qiskit Primitives.
Defining equivalence relationships
A common task in mapping abstract circuits to physical hardware and optimizing the result is to find equivalence relations that map a gate to a different basis set. Qiskit stores this information in a database class called EquivalenceLibrary.
EquivalenceLibrary(*[, base]) | A library providing a one-way mapping of Gates to their equivalent implementations as QuantumCircuits. |
Qiskit ships with a large set of predefined equivalence relationships for all of its standard gates. This base library is called StandardEquivalenceLibrary, and should be treated as immutable.
qiskit.circuit.StandardEquivalenceLibrary
A EquivalenceLibrary that stores of all Qiskit’s built-in standard gate relationships. You should not mutate this, but instead either create your own EquivalenceLibrary using this one as its base, or modify the global-state SessionEquivalenceLibrary.
Qiskit also defines a shared global-state object, SessionEquivalenceLibrary, which is the default equivalences used by various places in Qiskit, most notably the BasisTranslator transpiler pass. You should feel free to add your own equivalences to this using its add_equivalence() method, and they will be automatically picked up by default instances of the BasisTranslator.
qiskit.circuit.SessionEquivalenceLibrary
The default instance of EquivalenceLibrary, which will be used by most Qiskit objects if no library is manually specified. You can feel free to add equivalences to this using add_equivalence(). It inherits all the built-in rules of StandardEquivalenceLibrary.
Generating random circuits
random_circuit
qiskit.circuit.random.random_circuit(num_qubits, depth, max_operands=4, measure=False, conditional=False, reset=False, seed=None)
Generate random circuit of arbitrary size and form.
This function will generate a random circuit by randomly selecting gates from the set of standard gates in qiskit.circuit.library.standard_gates. For example:
from qiskit.circuit.random import random_circuit
circ = random_circuit(2, 2, measure=True)
circ.draw(output='mpl')
Parameters
- num_qubits (int(opens in a new tab)) – number of quantum wires
- depth (int(opens in a new tab)) – layers of operations (i.e. critical path length)
- max_operands (int(opens in a new tab)) – maximum qubit operands of each gate (between 1 and 4)
- measure (bool(opens in a new tab)) – if True, measure all qubits at the end
- conditional (bool(opens in a new tab)) – if True, insert middle measurements and conditionals
- reset (bool(opens in a new tab)) – if True, insert middle resets
- seed (int(opens in a new tab)) – sets random seed (optional)
Returns
constructed circuit
Return type
Raises
CircuitError – when invalid options given
Exceptions
Almost all circuit functions and methods will raise a CircuitError when encountering an error that is particular to usage of Qiskit (as opposed to regular typing or indexing problems, which will typically raise the corresponding standard Python error).
CircuitError
exception qiskit.circuit.CircuitError(*message)
Base class for errors raised while processing a circuit.
Set the error message.
Circuit conventions
When constructing circuits out of abstract objects and more concrete matrices, there are several possible conventions around bit-labelling, bit-ordering, and how the abstract tensor product is realized in concrete matrix algebra.
Qiskit’s conventions are:
- in bitstring representations, bits are labelled with the right-most bit in the string called and the left-most bit in the string of bits called .
- when using integers as bit-specifier indices in circuit-construction functions, the integer is treated as an index into
QuantumCircuit.qubits(orclbits). - when drawing circuits, we put the lowest-index bits on top.
- in statevector representations, we realize the abstract tensor product as the Kronecker product, and order the arguments to this such that the amplitude of computational-basis state , where is the bitstring interpreted as an integer, is at location
statevector[x]. - when controlling a gate, the control qubit(s) is placed first in the argument list, e.g. in the call
qc.cx(0, 1), qubit 0 will be the control and qubit 1 will be the target. Similarly, in the manual callqc.append(CXGate(), [0, 1]), qubit 0 will be the control and qubit 1 will be the target.
Let us illustrate these conventions with some examples.
Bit labelling
Take the circuit:
from qiskit import QuantumCircuit
qc = QuantumCircuit(5, 5)
qc.x(0)
qc.x(1)
qc.x(4)
qc.measure(range(5), range(5))This flips the states of qubits 0, 1 and 4 from to , then measures all qubits into the corresponding clbit using the computational () basis. If simulated noiselessly, the bitstring output from this circuit will be every time; qubits 0, 1, and 4 are flipped, and the “one” values in the bitstring are in the zeroth, first and fourth digits from the right.
In Qiskit, we would write the qubit state immediately before the measurement in ket-notation shorthand as . Note that the ket label matches the classical bitstring, and has the numeric binary value of 19.
If we draw this circuit, we will see that Qiskit places the zeroth qubit on the top of the circuit drawing:
qc.draw("mpl")
Matrix representations
Statevectors are defined in the convention that for a two-level system, the relationship between abstract representation and matrix representation is such that
where and are complex numbers. We store the statevector as a 1D Numpy ndarray(opens in a new tab) with data sv = [alpha, beta], i.e. sv[0] == alpha and sv[1] == beta; note that the indices into the statevector match the ket labels.
We construct the tensor product of two qubit states(opens in a new tab) in matrix algebra using the Kronecker product(opens in a new tab), with qubit 0 on the right and qubit 1 on the left, such that the basis state (where is the integer interpretation of the bitstring) has its non-zero term in the statevector sv at sv[x]:
import numpy
from qiskit import QuantumCircuit
from qiskit.quantum_info import Statevector
state_0 = [1, 0] # defined representation of |0>
state_1 = [0, 1] # defined representation of |1>
# Circuit that creates basis state |10011>, where
# binary 10011 has the decimal value 19.
qc = QuantumCircuit(5)
qc.x(0)
qc.x(1)
qc.x(4)
qiskit_sv = Statevector(qc)
# List index 'n' corresponds to qubit 'n'.
individual_states = [
state_1,
state_1,
state_0,
state_0,
state_1,
]
# Start from a scalar.
manual_sv = [1]
for qubit_state in individual_states:
# Each new qubit goes "on the left".
manual_sv = numpy.kron(qubit_state, manual_sv)
# Now `qiskit_sv` and `manual_sv` are the same, and:
assert manual_sv[19] == 1
assert qiskit_sv[19] == 1This feeds through to the matrix representation of operators, and joins with the conventions on bit orders for controlled operators. For example, the matrix form of CXGate is:
import numpy
from qiskit.circuit.library import CXGate
numpy.array(CXGate())This might be different to other matrix representations you have seen for , but recall that the choice of matrix representation is conventional, and this form matches Qiskit’s conventions of control qubits come first and the tensor product is represented such that there is a correspondence between the index of the “one amplitude” and the bitstring value of a state.
In the case of multiple controls for a gate, such as for CCXGate, the ctrl_state argument is interpreted as the bitstring value of the control qubits, using the same zero-based labelling conventions. For example, given that the default ctrl_state is the all-ones bitstring, we can see that the matrix form of CCXGate with ctrl_state = 1 is the same as if we took the all-ones control-state CCXGate, but flipped the value of the higher indexed control qubit on entry and exist to the gate:
from qiskit import QuantumCircuit
from qiskit.quantum_info import Operator
# Build the natural representation of `CCX` with the
# control qubits being `[0, 1]`, relative to the
# bitstring state "01", such that qubit 0 must be in |1>
# and qubit 1 must be in |0>. The target qubit is 2.
ccx_natural = QuantumCircuit(3)
ccx_natural.ccx(0, 1, 2, ctrl_state=1)
# Build the same circuit in terms of the all-ones CCX.
# Note that we flip _qubit 1_, because that's the one
# that differs from the all-ones state.
ccx_relative = QuantumCircuit(3)
ccx_relative.x(1)
ccx_relative.ccx(0, 1, 2)
ccx_relative.x(1)
assert Operator(ccx_relative) == Operator(ccx_natural)In both these cases, the matrix form of CCXGate in ctrl_state = 1 is: