Statevector
class qiskit.quantum_info.Statevector(data, dims=None)
Bases: QuantumState, TolerancesMixin
Statevector class
Initialize a statevector object.
Parameters
- or (data (np.array or list(opens in a new tab) orStatevector orOperator orQuantumCircuit) – qiskit.circuit.Instruction): Data from which the statevector can be constructed. This can be either a complex vector, another statevector, a
Operatorwith only one column or aQuantumCircuitorInstruction. If the data is a circuit or instruction, the statevector is constructed by assuming that all qubits are initialized to the zero state. - dims (int(opens in a new tab) ortuple(opens in a new tab) orlist(opens in a new tab)) – Optional. The subsystem dimension of the state (See additional information).
Raises
QiskitError – if input data is not valid.
Additional Information:
The dims kwarg can be None, an integer, or an iterable of integers.
Iterable– the subsystem dimensions are the values in the list with the total number of subsystems given by the length of the list.IntorNone– the length of the input vector specifies the total dimension of the density matrix. If it is a power of two the state will be initialized as an N-qubit state. If it is not a power of two the state will have a single d-dimensional subsystem.
Attributes
atol
Default value: 1e-08
data
Return data.
dim
Return total state dimension.
num_qubits
Return the number of qubits if a N-qubit state or None otherwise.
rtol
Default value: 1e-05
settings
Return settings.
Methods
conjugate
copy
dims
draw
draw(output=None, **drawer_args)
Return a visualization of the Statevector.
repr: ASCII TextMatrix of the state’s __repr__.
text: ASCII TextMatrix that can be printed in the console.
latex: An IPython Latex object for displaying in Jupyter Notebooks.
latex_source: Raw, uncompiled ASCII source to generate array using LaTeX.
qsphere: Matplotlib figure, rendering of statevector using plot_state_qsphere().
hinton: Matplotlib figure, rendering of statevector using plot_state_hinton().
bloch: Matplotlib figure, rendering of statevector using plot_bloch_multivector().
city: Matplotlib figure, rendering of statevector using plot_state_city().
paulivec: Matplotlib figure, rendering of statevector using plot_state_paulivec().
Parameters
- output (str(opens in a new tab)) – Select the output method to use for drawing the state. Valid choices are repr, text, latex, latex_source, qsphere, hinton, bloch, city, or paulivec. Default is repr. Default can be changed by adding the line
state_drawer = <default>to~/.qiskit/settings.confunder[default]. - drawer_args – Arguments to be passed directly to the relevant drawing function or constructor (TextMatrix(), array_to_latex(), plot_state_qsphere(), plot_state_hinton() or plot_bloch_multivector()). See the relevant function under qiskit.visualization for that function’s documentation.
Returns
matplotlib.Figure or str(opens in a new tab) or TextMatrix or IPython.display.Latex: Drawing of the Statevector.
Raises
ValueError(opens in a new tab) – when an invalid output method is selected.
Examples
Plot one of the Bell states
from numpy import sqrt
from qiskit.quantum_info import Statevector
sv=Statevector([1/sqrt(2), 0, 0, -1/sqrt(2)])
sv.draw(output='hinton')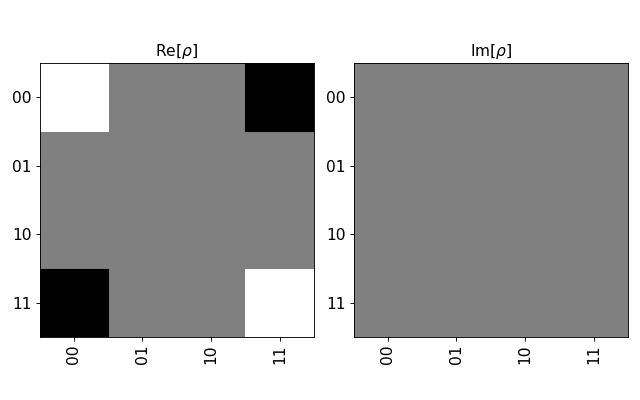
equiv
equiv(other, rtol=None, atol=None)
Return True if other is equivalent as a statevector up to global phase.
If other is not a Statevector, but can be used to initialize a statevector object, this will check that Statevector(other) is equivalent to the current statevector up to global phase.
Parameters
- other (Statevector) – an object from which a
Statevectorcan be constructed. - rtol (float(opens in a new tab)) – relative tolerance value for comparison.
- atol (float(opens in a new tab)) – absolute tolerance value for comparison.
Returns
True if statevectors are equivalent up to global phase.
Return type
evolve
evolve(other, qargs=None)
Evolve a quantum state by the operator.
Parameters
- other (Operator |QuantumCircuit |circuit.Instruction) – The operator to evolve by.
- qargs (list(opens in a new tab)) – a list of Statevector subsystem positions to apply the operator on.
Returns
the output quantum state.
Return type
Raises
QiskitError – if the operator dimension does not match the specified Statevector subsystem dimensions.
expand
expand(other)
Return the tensor product state other ⊗ self.
Parameters
other (Statevector) – a quantum state object.
Returns
the tensor product state other ⊗ self.
Return type
Raises
QiskitError – if other is not a quantum state.
expectation_value
expectation_value(oper, qargs=None)
Compute the expectation value of an operator.
Parameters
- oper (Operator) – an operator to evaluate expval of.
- qargs (None or list(opens in a new tab)) – subsystems to apply operator on.
Returns
the expectation value.
Return type
from_instruction
classmethod from_instruction(instruction)
Return the output statevector of an instruction.
The statevector is initialized in the state of the same number of qubits as the input instruction or circuit, evolved by the input instruction, and the output statevector returned.
Parameters
instruction (qiskit.circuit.Instruction orQuantumCircuit) – instruction or circuit
Returns
The final statevector.
Return type
Raises
QiskitError – if the instruction contains invalid instructions for the statevector simulation.
from_int
static from_int(i, dims)
Return a computational basis statevector.
Parameters
- i (int(opens in a new tab)) – the basis state element.
- dims (int(opens in a new tab) ortuple(opens in a new tab) orlist(opens in a new tab)) – The subsystem dimensions of the statevector (See additional information).
Returns
The computational basis state .
Return type
Additional Information:
The dims kwarg can be an integer or an iterable of integers.
Iterable– the subsystem dimensions are the values in the list with the total number of subsystems given by the length of the list.Int– the integer specifies the total dimension of the state. If it is a power of two the state will be initialized as an N-qubit state. If it is not a power of two the state will have a single d-dimensional subsystem.
from_label
classmethod from_label(label)
Return a tensor product of Pauli X,Y,Z eigenstates.
| Label | Statevector |
|---|
| "0" | |
| "1" | |
| "+" | |
| "-" | |
| "r" | |
| "l" | |
Parameters
label (string) – a eigenstate string ket label (see table for allowed values).
Returns
The N-qubit basis state density matrix.
Return type
Raises
QiskitError – if the label contains invalid characters, or the length of the label is larger than an explicitly specified num_qubits.
inner
inner(other)
Return the inner product of self and other as .
Parameters
other (Statevector) – a quantum state object.
Returns
the inner product of self and other, .
Return type
np.complex128
Raises
QiskitError – if other is not a quantum state or has different dimension.
is_valid
is_valid(atol=None, rtol=None)
Return True if a Statevector has norm 1.
Return type
measure
measure(qargs=None)
Measure subsystems and return outcome and post-measure state.
Note that this function uses the QuantumStates internal random number generator for sampling the measurement outcome. The RNG seed can be set using the seed() method.
Parameters
qargs (list(opens in a new tab) or None) – subsystems to sample measurements for, if None sample measurement of all subsystems (Default: None).
Returns
the pair (outcome, state) where outcome is the
measurement outcome string label, and state is the collapsed post-measurement state for the corresponding outcome.
Return type
probabilities
probabilities(qargs=None, decimals=None)
Return the subsystem measurement probability vector.
Measurement probabilities are with respect to measurement in the computation (diagonal) basis.
Parameters
- qargs (None or list(opens in a new tab)) – subsystems to return probabilities for, if None return for all subsystems (Default: None).
- decimals (None or int(opens in a new tab)) – the number of decimal places to round values. If None no rounding is done (Default: None).
Returns
The Numpy vector array of probabilities.
Return type
np.array
Examples
Consider a 2-qubit product state .
from qiskit.quantum_info import Statevector
psi = Statevector.from_label('+0')
# Probabilities for measuring both qubits
probs = psi.probabilities()
print('probs: {}'.format(probs))
# Probabilities for measuring only qubit-0
probs_qubit_0 = psi.probabilities([0])
print('Qubit-0 probs: {}'.format(probs_qubit_0))
# Probabilities for measuring only qubit-1
probs_qubit_1 = psi.probabilities([1])
print('Qubit-1 probs: {}'.format(probs_qubit_1))probs: [0.5 0. 0.5 0. ]
Qubit-0 probs: [1. 0.]
Qubit-1 probs: [0.5 0.5]We can also permute the order of qubits in the qargs list to change the qubit position in the probabilities output
from qiskit.quantum_info import Statevector
psi = Statevector.from_label('+0')
# Probabilities for measuring both qubits
probs = psi.probabilities([0, 1])
print('probs: {}'.format(probs))
# Probabilities for measuring both qubits
# but swapping qubits 0 and 1 in output
probs_swapped = psi.probabilities([1, 0])
print('Swapped probs: {}'.format(probs_swapped))probs: [0.5 0. 0.5 0. ]
Swapped probs: [0.5 0.5 0. 0. ]probabilities_dict
probabilities_dict(qargs=None, decimals=None)
Return the subsystem measurement probability dictionary.
Measurement probabilities are with respect to measurement in the computation (diagonal) basis.
This dictionary representation uses a Ket-like notation where the dictionary keys are qudit strings for the subsystem basis vectors. If any subsystem has a dimension greater than 10 comma delimiters are inserted between integers so that subsystems can be distinguished.
Parameters
- qargs (None or list(opens in a new tab)) – subsystems to return probabilities for, if None return for all subsystems (Default: None).
- decimals (None or int(opens in a new tab)) – the number of decimal places to round values. If None no rounding is done (Default: None).
Returns
The measurement probabilities in dict (ket) form.
Return type
purity
reset
reset(qargs=None)
Reset state or subsystems to the 0-state.
Parameters
qargs (list(opens in a new tab) or None) – subsystems to reset, if None all subsystems will be reset to their 0-state (Default: None).
Returns
the reset state.
Return type
Additional Information:
If all subsystems are reset this will return the ground state on all subsystems. If only a some subsystems are reset this function will perform a measurement on those subsystems and evolve the subsystems so that the collapsed post-measurement states are rotated to the 0-state. The RNG seed for this sampling can be set using the seed() method.
reverse_qargs
reverse_qargs()
Return a Statevector with reversed subsystem ordering.
For a tensor product state this is equivalent to reversing the order of tensor product subsystems. For a statevector the returned statevector will be .
Returns
the Statevector with reversed subsystem order.
Return type
sample_counts
sample_counts(shots, qargs=None)
Sample a dict of qubit measurement outcomes in the computational basis.
Parameters
- shots (int(opens in a new tab)) – number of samples to generate.
- qargs (None or list(opens in a new tab)) – subsystems to sample measurements for, if None sample measurement of all subsystems (Default: None).
Returns
sampled counts dictionary.
Return type
Additional Information:
This function samples measurement outcomes using the measure
probabilities()for the current state and qargs. It does not actually implement the measurement so the current state is not modified.The seed for random number generator used for sampling can be set to a fixed value by using the stats
seed()method.
sample_memory
sample_memory(shots, qargs=None)
Sample a list of qubit measurement outcomes in the computational basis.
Parameters
- shots (int(opens in a new tab)) – number of samples to generate.
- qargs (None or list(opens in a new tab)) – subsystems to sample measurements for, if None sample measurement of all subsystems (Default: None).
Returns
list of sampled counts if the order sampled.
Return type
np.array
Additional Information:
This function samples measurement outcomes using the measure
probabilities()for the current state and qargs. It does not actually implement the measurement so the current state is not modified.The seed for random number generator used for sampling can be set to a fixed value by using the stats
seed()method.
seed
tensor
tensor(other)
Return the tensor product state self ⊗ other.
Parameters
other (Statevector) – a quantum state object.
Returns
the tensor product operator self ⊗ other.
Return type
Raises
QiskitError – if other is not a quantum state.
to_dict
to_dict(decimals=None)
Convert the statevector to dictionary form.
This dictionary representation uses a Ket-like notation where the dictionary keys are qudit strings for the subsystem basis vectors. If any subsystem has a dimension greater than 10 comma delimiters are inserted between integers so that subsystems can be distinguished.
Parameters
decimals (None or int(opens in a new tab)) – the number of decimal places to round values. If None no rounding is done (Default: None).
Returns
the dictionary form of the Statevector.
Return type
Example
The ket-form of a 2-qubit statevector
from qiskit.quantum_info import Statevector
psi = Statevector.from_label('-0')
print(psi.to_dict()){'00': (0.7071067811865475+0j), '10': (-0.7071067811865475+0j)}For non-qubit subsystems the integer range can go from 0 to 9. For example in a qutrit system
import numpy as np
from qiskit.quantum_info import Statevector
vec = np.zeros(9)
vec[0] = 1 / np.sqrt(2)
vec[-1] = 1 / np.sqrt(2)
psi = Statevector(vec, dims=(3, 3))
print(psi.to_dict()){'00': (0.7071067811865475+0j), '22': (0.7071067811865475+0j)}For large subsystem dimensions delimiters are required. The following example is for a 20-dimensional system consisting of a qubit and 10-dimensional qudit.
import numpy as np
from qiskit.quantum_info import Statevector
vec = np.zeros(2 * 10)
vec[0] = 1 / np.sqrt(2)
vec[-1] = 1 / np.sqrt(2)
psi = Statevector(vec, dims=(2, 10))
print(psi.to_dict()){'00': (0.7071067811865475+0j), '91': (0.7071067811865475+0j)}to_operator
trace
trace()
Return the trace of the quantum state as a density matrix.
Return type
float64