QFT
class qiskit.circuit.library.QFT(num_qubits=None, approximation_degree=0, do_swaps=True, inverse=False, insert_barriers=False, name=None)
Bases: BlueprintCircuit
Quantum Fourier Transform Circuit.
The Quantum Fourier Transform (QFT) on qubits is the operation
The circuit that implements this transformation can be implemented using Hadamard gates on each qubit, a series of controlled-U1 (or Z, depending on the phase) gates and a layer of Swap gates. The layer of Swap gates can in principle be dropped if the QFT appears at the end of the circuit, since then the re-ordering can be done classically. They can be turned off using the do_swaps attribute.
For 4 qubits, the circuit that implements this transformation is:
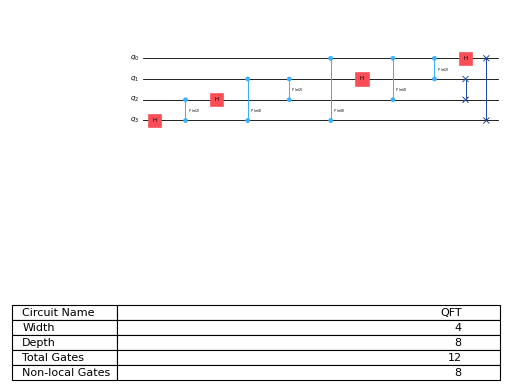
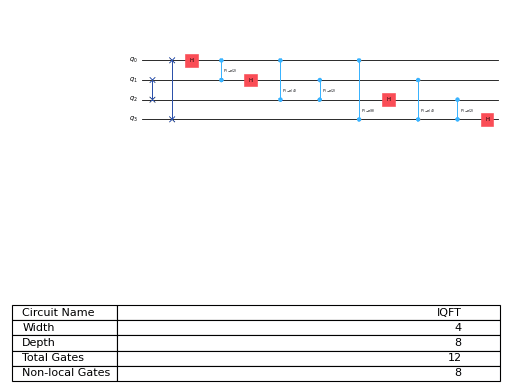
The inverse QFT can be obtained by calling the inverse method on this class. The respective circuit diagram is:
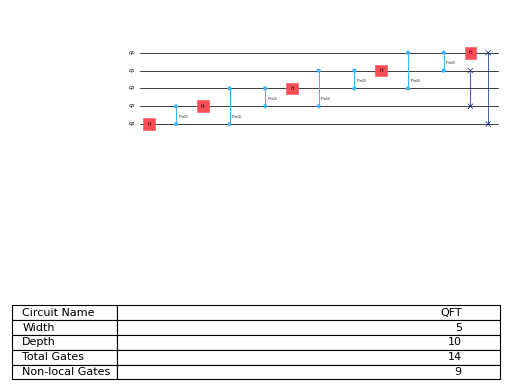
One method to reduce circuit depth is to implement the QFT approximately by ignoring controlled-phase rotations where the angle is beneath a threshold. This is discussed in more detail in https://arxiv.org/abs/quant-ph/9601018(opens in a new tab) or https://arxiv.org/abs/quant-ph/0403071(opens in a new tab).
Here, this can be adjusted using the approximation_degree attribute: the smallest approximation_degree rotation angles are dropped from the QFT. For instance, a QFT on 5 qubits with approximation degree 2 yields (the barriers are dropped in this example):
Construct a new QFT circuit.
Parameters
- num_qubits (int(opens in a new tab) | None) – The number of qubits on which the QFT acts.
- approximation_degree (int(opens in a new tab)) – The degree of approximation (0 for no approximation).
- do_swaps (bool(opens in a new tab)) – Whether to include the final swaps in the QFT.
- inverse (bool(opens in a new tab)) – If True, the inverse Fourier transform is constructed.
- insert_barriers (bool(opens in a new tab)) – If True, barriers are inserted as visualization improvement.
- name (str(opens in a new tab) | None) – The name of the circuit.
Attributes
ancillas
A list of AncillaQubits in the order that they were added. You should not mutate this.
approximation_degree
The approximation degree of the QFT.
Returns
The currently set approximation degree.
calibrations
Return calibration dictionary.
The custom pulse definition of a given gate is of the form {'gate_name': {(qubits, params): schedule}}
clbits
A list of Clbits in the order that they were added. You should not mutate this.
data
do_swaps
Whether the final swaps of the QFT are applied or not.
Returns
True, if the final swaps are applied, False if not.
global_phase
The global phase of the current circuit scope in radians.
insert_barriers
Whether barriers are inserted for better visualization or not.
Returns
True, if barriers are inserted, False if not.
instances
Default value: 214
layout
Return any associated layout information about the circuit
This attribute contains an optional TranspileLayout object. This is typically set on the output from transpile() or PassManager.run() to retain information about the permutations caused on the input circuit by transpilation.
There are two types of permutations caused by the transpile() function, an initial layout which permutes the qubits based on the selected physical qubits on the Target, and a final layout which is an output permutation caused by SwapGates inserted during routing.
metadata
Arbitrary user-defined metadata for the circuit.
Qiskit will not examine the content of this mapping, but it will pass it through the transpiler and reattach it to the output, so you can track your own metadata.
num_ancillas
Return the number of ancilla qubits.
num_captured_vars
The number of real-time classical variables in the circuit marked as captured from an enclosing scope.
This is the length of the iter_captured_vars() iterable. If this is non-zero, num_input_vars must be zero.
num_clbits
Return number of classical bits.
num_declared_vars
The number of real-time classical variables in the circuit that are declared by this circuit scope, excluding inputs or captures.
This is the length of the iter_declared_vars() iterable.
num_input_vars
The number of real-time classical variables in the circuit marked as circuit inputs.
This is the length of the iter_input_vars() iterable. If this is non-zero, num_captured_vars must be zero.
num_parameters
num_qubits
The number of qubits in the QFT circuit.
Returns
The number of qubits in the circuit.
num_vars
The number of real-time classical variables in the circuit.
This is the length of the iter_vars() iterable.
op_start_times
Return a list of operation start times.
This attribute is enabled once one of scheduling analysis passes runs on the quantum circuit.
Returns
List of integers representing instruction start times. The index corresponds to the index of instruction in QuantumCircuit.data.
Raises
AttributeError(opens in a new tab) – When circuit is not scheduled.
parameters
prefix
Default value: 'circuit'
qregs
Type: list[QuantumRegister]
A list of the QuantumRegisters in this circuit. You should not mutate this.
qubits
A list of Qubits in the order that they were added. You should not mutate this.
name
Type: str
A human-readable name for the circuit.
cregs
Type: list[ClassicalRegister]
A list of the ClassicalRegisters in this circuit. You should not mutate this.
duration
Type: int | float | None
The total duration of the circuit, set by a scheduling transpiler pass. Its unit is specified by unit.
unit
The unit that duration is specified in.
Methods
inverse
inverse(annotated=False)
Invert this circuit.
Parameters
annotated (bool(opens in a new tab)) – indicates whether the inverse gate can be implemented as an annotated gate. The value of this argument is ignored as the inverse of a QFT is an IQFT which is just another instance of QFT.
Returns
The inverted circuit.
Return type
is_inverse
is_inverse()
Whether the inverse Fourier transform is implemented.
Returns
True, if the inverse Fourier transform is implemented, False otherwise.
Return type